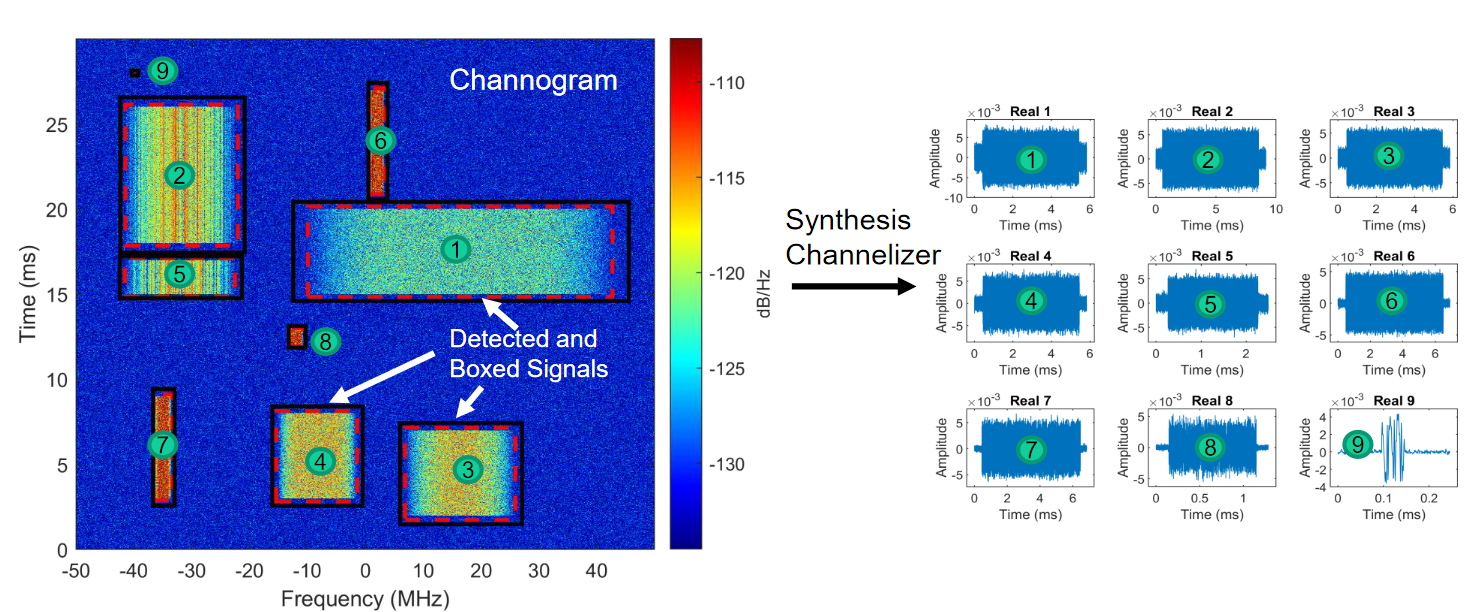
The windowed fast Fourier transform (FFT) is the ubiquitous tool for spectral analysis because it is fast and easy to use. In this paper we will show how the polyphase channelizer can replace the FFT for spectral analysis and produce estimates of the power spectral density (PSD) and the short-time Fourier transform (STFT) spectrogram. We refer to the polyphase channelizer equivalents of these estimates respectively as the channelizer power spectral density (cPSD) and the channogram. It will be shown that the spectral resolution of the cPSD and channogram improves upon the well-established FFT-based estimators for a given FFT length while introducing minimal processing overhead. We will then discuss Parseval's theorem equivalent for the polyphase channelizer. Finally, we will show how the polyphase channelizer leads to straightforward signal segregation and inversion back to time domain when signals of random and unknown center frequencies and bandwidth are encountered. This is an important enabler for real-time radio frequency (RF) signal classification using machine learning algorithms.